Computer systems affect diverse aspects of our lives today. From the mobile phones we use to the cars, trains and airplanes we ride and fly in, from the ATMs dispensing money to the EVMs used in elections, from the life-support systems in ICUs to railway signaling systems, (embedded) computer systems silently pervade our lives. Needless to say, software or hardware bugs in these systems can have wide ranging consequences, from mere inconvenience to even loss of lives. Being able to detect bugs in computer systems is therefore important, and being able to certify the absence of bugs is of immense practical value, especially in safety-critical systems. Although testing remains the mainstream approach for bug-hunting, exhaustive testing is impractical for all but the simplest of systems.For example, to comprehensively test a module that claims to add two 64-bit integers requires providing 2128 test cases. Even if each test could be completed in 1 femtosecond, this would require approximately 1016 years! How do we then show that much more complex systems like railway signal controllers or the autopilot of an aircraft, on which the safety of lives are entrusted, are free of bugs?At the Centre for Formal Design and Verification of Software (CFDVS), IIT
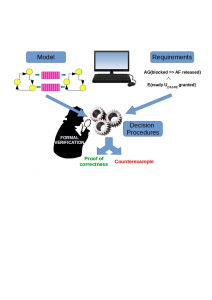
Bombay, we focus on scalable formal methods to address questions like the one above. Loosely speaking, formal methods are mathematical and computational techniques for proving properties of systems, without depending on test cases. Given a system, its behaviour is modeled using a mathematical formalism, viz. automata, state transition systems, process algebras, etc. The requirement (what it is supposed to do) is also captured in an unambiguous way, using formalisms like logic, automata, constraint systems, property specification languages, etc. The mathematical object representing the requirement is then checked against the mathematical object representing the model to determine if the model permits any behaviour that violates the requirement. This is done by specialised algorithms that try to achieve a fine balance between providing correctness guarantees and performance that scales large problem instances. The unique strength of formal methods is its ability to weed out bugs in deep corners of the input space that may elude even the most experienced engineers. After all, we’d really like to rest assured the next time we travel in a train or fly in an airplane that the computers on which we entrust our safety are really doing what they are meant to do.