This invention presents a novel algorithm for synthesizing exact solutions to constrained optimal control problems in mechanical systems such as robotics, aerial vehicles, and satellites. Unlike traditional methods limited to Euclidean spaces, this approach addresses the complexities of systems evolving on manifolds. The algorithm employing discrete mechanics for exact discretization developed a discrete-time Pontryagin maximum principle for variational integrators, as well as a new multiple shooting technique to solve constrained two-point boundary value problems efficiently. This results in precise, robust, and computationally efficient solutions for large-angle attitude maneuvers, surpassing the accuracy and applicability of existing methods. The technology has significant implications for enhancing the performance and reliability of safety-critical systems in aerospace and robotics industries.
Figure 1. The state trajectory and the corresponding optimal control for the maneuver T1
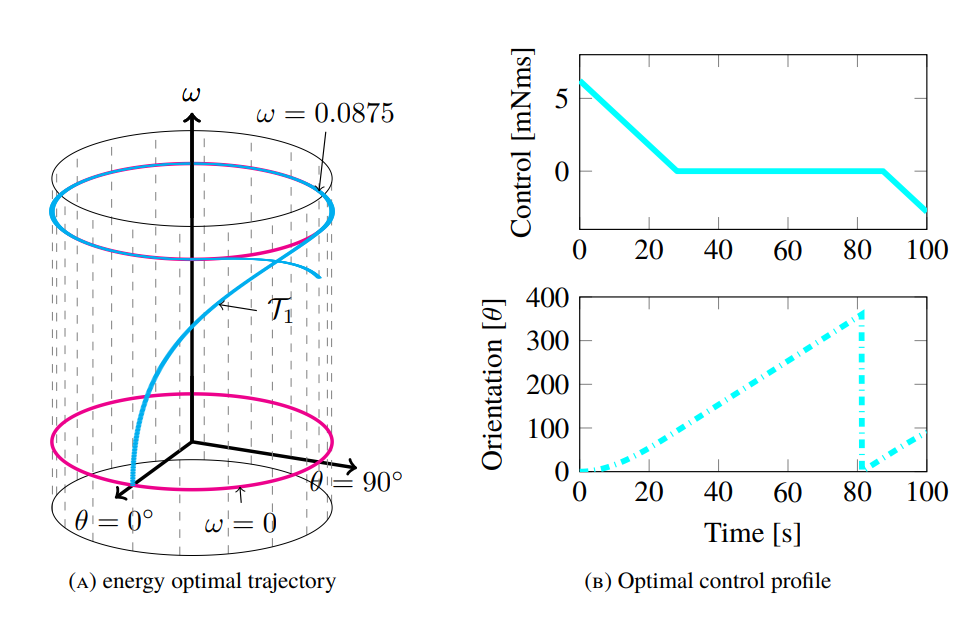
The existing techniques for solving trajectory optimization problems arising in attitude control of a satellite/spacecraft with actuation and momentum constraints are either inexact or computationally intractable. In this work, the exact discrete-time model for the system is derived using discrete mechanics (a structure preserving discretization scheme) and necessary conditions for optimality are established. Subsequently, the resulting two-point boundary value problem is solved using a novel projected multiple shooting method, resulting in both an exact and a computationally tractable solution.
A new algorithm has been designed to find optimal control functions for large-angle optimal attitude maneuvers, representing a significant advancement in the field. Some of the innovative features introduced by this approach are:
- Exact Discretization: The use of discrete mechanics ensures that the state space structure is preserved under discretization, leading to more accurate models.
- Discrete-time PMP: A new Pontryagin maximum principle tailored for discrete-time systems on matrix Lie groups, addressing the challenges of systems evolving on manifolds.
- Multiple Shooting Technique: A novel multiple shooting method that efficiently solves the resulting constrained two-point boundary value problems, robust to initial guesses and suitable for parallel computation.
- Handling Large-angle Maneuvers: Unlike traditional methods, this algorithm can handle large-angle attitude maneuvers without approximation errors.
NA
This algorithm has been extensively tested in numerical simulations. A 200 page extensive documentation has been drafted along with ISRO.
9
The proposed technology can significantly enhance the precision and efficiency of attitude control in safety-critical systems like satellites and aerial vehicles, leading to improved mission success rates, reduced costs, and enhanced capabilities for scientific and commercial applications in space exploration, telecommunications, and Earth observation.
- Spacecraft maneuvers and attitude control: Precise control of satellite orientation for tasks such as Earth observation, geo-spatial data collection, communications, and scientific missions
- Robotic manipulators: Optimal control of robotic arms in manufacturing, medical surgery, and automated systems
- Aerial Vehicles: Enhanced maneuverability and control of drones and other unmanned aerial systems in complex environments
202121002971
510833